|
Sea 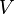 un
espacio vectorial sobre el campo F. Un subespacio
vectorial un
espacio vectorial sobre el campo F. Un subespacio
vectorial 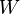 de de 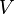 es
un subconjunto de es
un subconjunto de 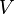 tal
que es espacio vectorial sobre F con las mismas
operaciones definidas en tal
que es espacio vectorial sobre F con las mismas
operaciones definidas en 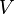 ,
es decir que cumple las 8 propiedades de espacio
vectorial. ,
es decir que cumple las 8 propiedades de espacio
vectorial.
Teorema
(de caracterización) Sea 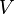 un espacio
vectorial sobre F, W es subespacio vectorial de si y
solo si se cumplen las siguientes propiedades: un espacio
vectorial sobre F, W es subespacio vectorial de si y
solo si se cumplen las siguientes propiedades:
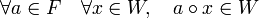 
Demostración
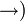 Es evidente, porque las
operaciones Es evidente, porque las
operaciones 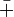 y y  son
operaciones en son
operaciones en 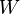 . .
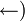 Las
8 propiedades de espacio vectorial se cumplen en Las
8 propiedades de espacio vectorial se cumplen en 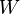 porque se
cumplen en porque se
cumplen en 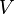 . .
Corolario Un
subconjunto 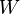 no
vacío de no
vacío de 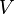 es subespacio vectorial si y solo
si, para cada es subespacio vectorial si y solo
si, para cada 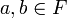 y para cada y para cada 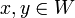 se
cumple se
cumple
-
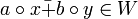 . .
|