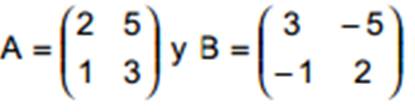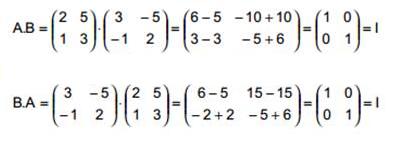Se dice que una matriz cuadrada A es inversible, si existe una matriz B con la propiedad de que:

                                           A•B=B•A=I                              

siendo I la matriz identidad.

Denominamos a la matriz B la inversa de A y la denotamos por A^-1 .

Una matriz se dice que es inversible o regular si posee inversa. En caso contrario, se dice que es singular.

 Ejemplo:

Supongamos:

Entonces:

Puesto que AB = BA = I, A y B son inversibles, siendo cada una la inversa de la otra.

El problema de encontrar elementos inversos para el producto de matrices tiene como primer inconveniente que, para empezar, no siempre dadas dos matrices A y B, que podamos hacer el producto A·B significa que podamos hacer el producto B·A 

Además, que dos matrices sean inversas una de la otra significa, en particular, que el producto ha de dar como resultado la matriz identidad. Si recordamos la definición, la matriz identidad es aquélla cuyos elementos son nulos salvo los de la diagonal, que son 1, y, además, esto es importante, dicha matriz es cuadrada. El hecho de que la matriz identidad sea cuadrada nos va a restringir mucho el conjunto de matrices para las que podremos hablar de inversión. 

Vamos a ver qué primera condición han de cumplir dos matrices A y B para que sean la una inversa de la otra. Esto, como sabemos, significa que A·B = B·A = I, donde I denota a la matriz identidad. Las matrices serán, en principio, A de orden mxn y B de orden pxq. 

Sin embargo, por definición del producto de matrices, se debe cumplir que n=p para poder hacer la multiplicación A·B. Sabemos, además, que esta matriz será de orden mxq. Pero también tenemos que poder hacer el producto B·A, lo que implica que debe ser m=q. Así pues, la matriz A será de orden mxn, y la matriz B será de orden nxm.

El producto A·B será de orden mxm, y el producto B·A será de orden nxn. Además, ambos productos han de dar como resultado la matriz identidad, y ésta es cuadrada, lo que obliga a que m=n, es decir, a que para poder hablar de inversión de una matriz, la matriz ha de ser cuadrada. Sin embargo, es una condición necesaria pero no suficiente; esto es, no toda matriz que sea cuadrada tiene matriz inversa. No es la única condición que se exige a la matriz.