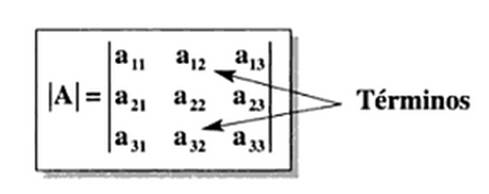
Determinante de una matriz cuadrada A es la suma de todos los productos de los elementos de dicha matriz, de forma que se elija un término de cada fila y uno de cada columna sin repetir dos de la misma fila o dos de la misma columna, afectados del signo según que las inversiones de los indicativos de columnas, una vez ordenados los de filas natural, sean pares o no.

No debemos preocuparnos excesivamente por esta definición, puesto que tanto la elección de los productos como los signos de las inversiones se realizan de una forma mecánica como tendremos ocasión de comprobar a medida que avancemos en el estudio de esta teoría.

Los determinantes se denotan situando los términos de la matriz A de la que proceden, entre dos líneas, es decir:

su determinante será:

 ORDEN DE UN DETERMINANTE

 Es el numero de filas o de columnas que lo componen. Lógicamente coincide con el orden de la matriz correspondiente.