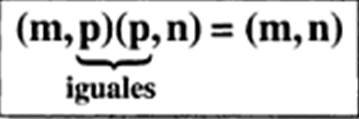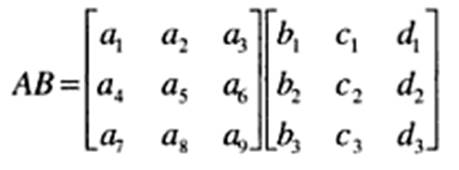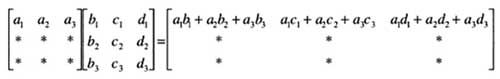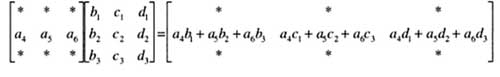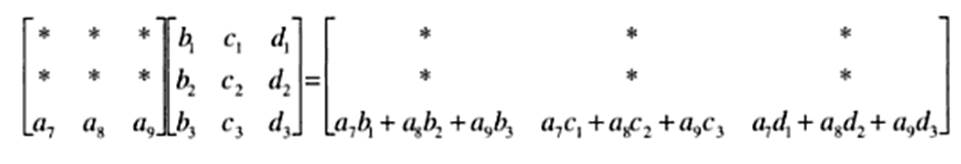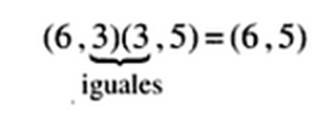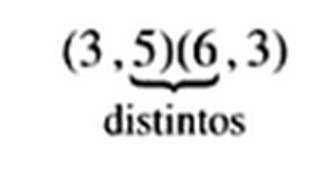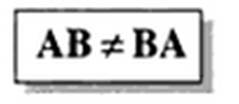3.2.3.- Producto entre matrices
|
Para multiplicar dos matrices será necesario cumplir el siguiente requisito: El número de columnas de la primera matriz deberá ser igual al número de filas de la segunda.
Donde el orden de la primera matriz es (m,p), y el de la segunda matriz es (p, n), por tanto el orden de la matriz resultante será (m,n). La forma de operar dos matrices AB será la siguiente: FILAS DE LA PRIMERA MATRIZ (A) POR COLUMNAS DE LA SEGUNDA MATRIZ (B), es decir: La primera fila de A por todas las columnas de B, generará la primera fila de la matriz producto AB. La segunda fila de A por todas las columnas de B, generará la segunda fila de la matriz producto AB. La tercera fila de A por todas las columnas de B, generará la tercera fila de la matriz producto AB, y así sucesivamente. Para entender cómodamente el proceso, utilizaremos una matriz genérica de tercer orden. Con dicha matriz la operación AB será como sigue.
Fijémonos solo en la generación de la primera fila de la matriz producto.
A continuación nos fijaremos solo en la generación de la segunda fila de la matriz producto.
Por ultimo, nos fijaremos solo en la generación de la tercera fila de la matriz producto.
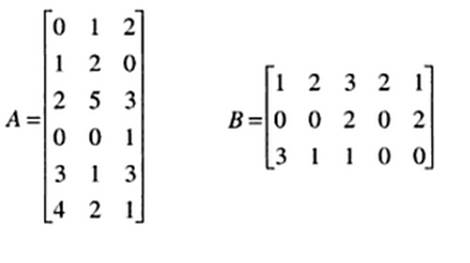
En general se dice que en el producto de dos matrices AB, la matriz A premultiplica a la matriz B y que la matriz B postmultiplica a la matriz A. Ejemplo: Comprobar si son multiplicables las matrices A y B.
Para comprobar si son o no multiplicables, se deberá observar que los órdenes de ambas matrices en la disposición AB cumplirán:
es decir, como el orden de la primera es de (6,3) y el orden de la segunda es (3,5), serán multiplicables y el orden de la matriz producto matriz será (6,5). En el caso contrario, es decir BA, no es posible, dado que no se cumple de que 5 y 6 no son iguales, es decir:
de esto se deduce que el producto de matrices no tiene en general la propiedad conmutativa, esto es:
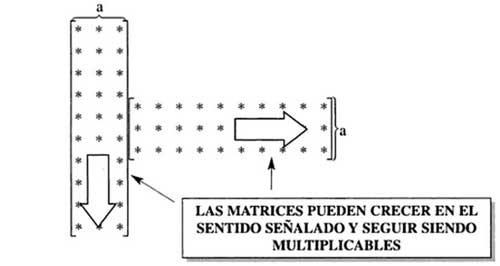
Existe un tipo de matrices denominados conmutables que si cumplen la propiedad conmutativa. En el producto de dos matrices, el requisito de que el numero de columnas de la primera matriz deberá ser igual al numero de filas de la segunda, permite que las matrices a multiplicar puedan ser tan grandes como se quiera en el sentido señalado en el siguiente esquema:
Es
decir que mientras se cumpla que el numero de columnas
de la primera (a) sea igual al numero de filas de la
segunda (a), el producto de matrices podrá ser
efectuado. |