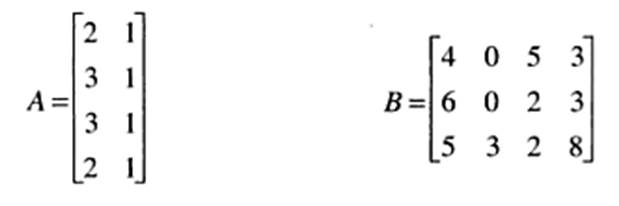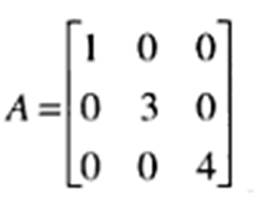3.1.1.- Tipos de matrices
|
La nomenclatura de los distintos tipos de matrices es la siguiente: Una matriz m x 1 se denomina matriz columna o matriz vector, por tener m renglones y 1 columna. Su orden será: m x 1
Una matriz de 1 x n se llama: MATRIZ RENGLÓN, por tener 1 renglón y “n” columnas. Su orden será: 1 x n.
1. MATRIZ CUADRADA Se dice que una matriz A es cuadrada si tiene el mismo número de filas que de columnas. Ejemplos de matriz cuadrada:
2. MATRIZ RECTANGULAR Es la que tiene distinto número de filas que de columnas.
Ejemplo: Hallar los órdenes de las siguientes matrices rectangulares:
el orden de la matriz A es (4,2) y el de la matriz B (3,4).
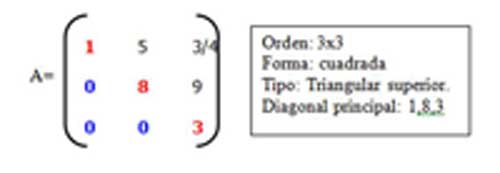
3.MATRIZ TRIANGULAR SUPERIOR Se dice que una matriz A es una matriz triangular superior si todos sus elementos debajo de la diagonal principal son cero.
La diagonal principal, se identifica en una matriz por tener el mismo orden en renglón y columnas, es decir: 1er renglón, 1ra columna. 2do renglón, 2da columna. 3er renglón, 3ra columna.
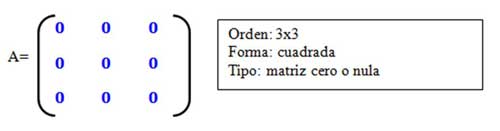
4. MATRIZ TRIANGULAR INFERIOR Se dice que es una matriz triangular inferior si es una matriz cuadrada en donde todos los elementos que están por encima de la diagonal principal son 0. 5. MATRIZ NULA O MATRIZ CERO Es la que tiene todos sus términos nulos. Puede tener cualquier orden.
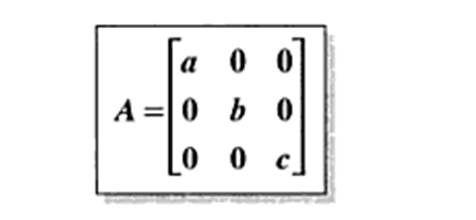
6. MATRIZ DIAGONAL
con a, b y c escalares cualquiera. Ejemplo. Escribir la matriz diagonal cuyos términos son 1, 3, y 4.
7. MATRIZ IDENTIDAD
Se dice que una “I” es una matriz identidad cuando los elementos que conforman la diagonal principal son siempre uno’s y sus demás elementos son cero, características importantes: su forma debe ser siempre cuadrada y no contener valores negativos. Ejemplo: 8. MATRIZ TRANSPUESTA
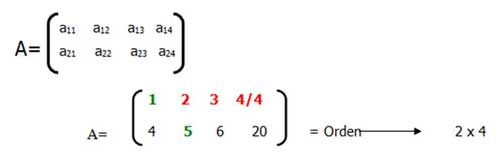
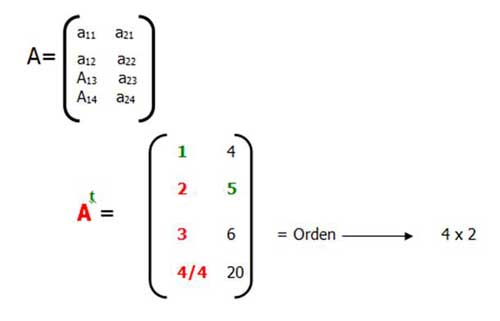
Se dice que una “A” es una matriz transpuesta cuando los elementos de los renglones pasan a ser columnas; y las columnas pasan a ser renglones; se identifica como At , y por lo tanto el orden o tamaño cambia. Ejemplo:
Al transponerla, queda como sigue:
Principal característica: su diagonal principal nunca cambia.
|





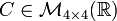

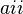 .
. y
y 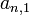 , como características, todos los elementos tienen la particularidad que sus subíndices suman (n+1), por ejemplo
, como características, todos los elementos tienen la particularidad que sus subíndices suman (n+1), por ejemplo 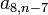 , donde 8 + (n - 7 ) = n + 1.
, donde 8 + (n - 7 ) = n + 1.