2.2.1.- Interpretación Geométrica
|
Caso
1: Tenemos el sistema de ecuaciones lineales:
a11x1 + a12x2 = c1 a21x1 + a22x2 = c2 Despejando
x2 de
ambas ecuaciones, tenemos:
x2 = ( -a11x1 + c1 ) / a12 = -( a11 / a12 )x1 + (c1 / a12 )
x2 = ( -a21x1 + c2 ) / a22 = -( a21 /
a22 )x1 + (
c2 / a22 )
De esta manera las ecuaciones se encuentran ahora en la forma de la ecuación de una línea recta, esto es:
x2 = pendiente x1 + intersección Estas líneas se pueden graficar en coordenadas cartesianas con x2 como la ordenada y x1 como la abscisa; los valores de x1 y x2 en la intersección de las líneas representa la solución del sistema.
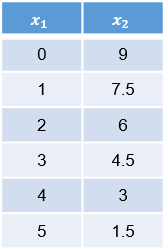
Ejemplo: 3x1 +
2x2 = 18 (1) -x1
+ 2x2 = 2
(2) De la ecuación (1),despejamos x2 x2 =
( -3x1 + 18 ) / 2 x2 =
(-3/2) x1 + 9
(3)
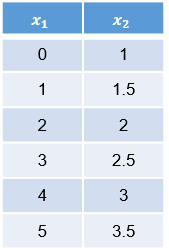
x2 = (x1 + 2)/2 x2 = (1/2)x1 + 1
(4)
Tabulamos las escuaciones 3 y 4 asignando valores a x1 Eccuación
3
Ecuación 4
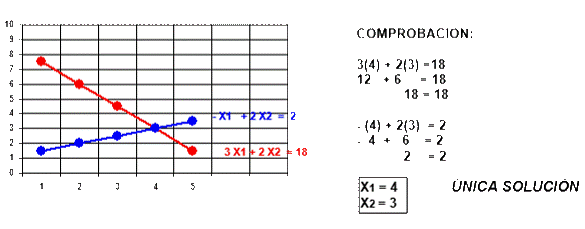
Comprobación: 3x1 +
2x2 = 18 --> 3(4)
+ 2(3) = 18 --> 12 + 6 = 18 --> 18=18 -x1
+ 2x2 = 2 -->
-(4) + 2(3) = 2 --> -4 + 6 = 2 --> 2 = 2
Caso
2:
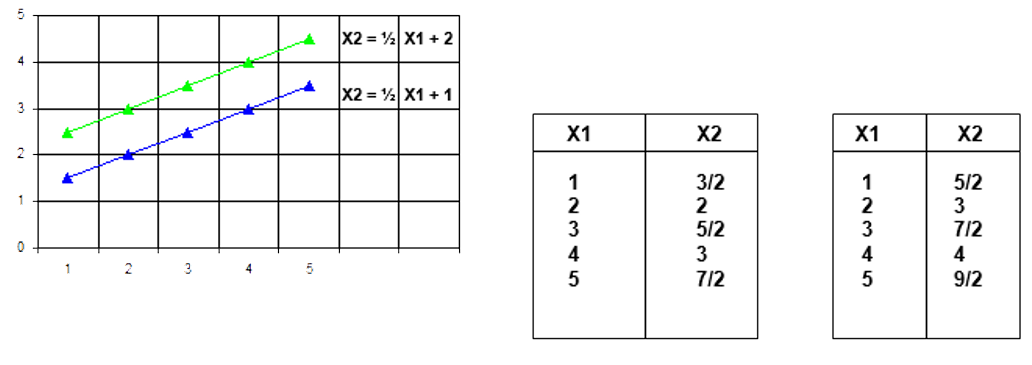
Cuando en el sistema de ecuaciones: a11x1 + a12x2 = c1 a21x1 + a22x2 = c2 a11 = a21 ; a12 = a22 y c1 es
diferente a c2;
En este caso se muestra un sistema de ecuaciones algebraicas lineales en el que las 2 ecuaciones representan 2 líneas paralelas en cuyo caso no existe solución ya que las 2 líneas jamás se cruzan.
Caso
3:
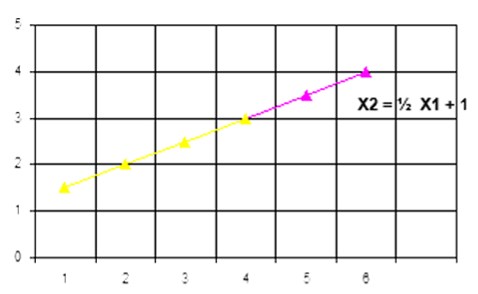
Cuando en el sistema de ecuaciones: a11x1 + a12x2 = c1 (1) a21x1 + a22x2 = c2 (2) Se
observa que la ecuación uno es multiplo o
submultiplo de la ecuación dos o visceversa,
ahora se tiene un sistema de 2 ecuaciones
algebraicas lineales en el que las líneas que
representa su gráfica, coinciden una sobre la otra
por lo que se establece que existe un número
infinito de soluciones, por ejemplo:
-1/2x1 + x2 = 1 -------> despejando x2 ----------------> x2 = (1/2)x1 + 1 -x1 + 2x1= 2 -------> despejando x2 ----------------> x2= (1/2)x1 + 1
|