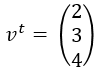4.1.- Concepto de Vector
|
Vector Al segmento de recta dirigido de P a Q se le conoce como vector.
Gráfica: 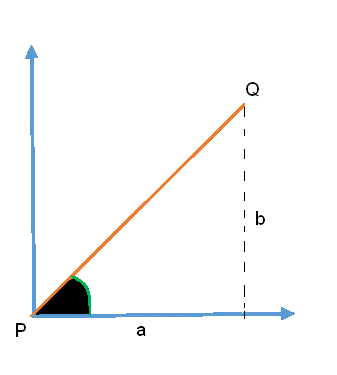
Un vector posee magnitud y dirección. | v | = (a2 + b2)1/2
tg
Definición
Algebraica de un vector: Es un conjunto
de elementos ordenados en renglon o columna.
Un
vector v en el plano xy es un par ordenado de números
reales (a,b). Los números a y b se conocen como las
componentes del vector v. El vector cero es (0,0). Observación 1: Con esta definición, un punto en el plano xy puede considerarse como un vector que se inicia en el origen y termina en ese punto. Observación 2: El vector cero tiene magnitud cero. Por tanto, como el punto inicial y el terminal coinciden decimos que el vector cero no tiene dirección. Observación 3: Enfatizamos que las definiciones 1 y 2 describen exactamente los mismos objetos, Cada punto de vista (geométrico y algebraico) tiene sus ventajas. La definición 2 es la definición de un vector con dos componentes que hemos venido usando hasta ahora.
Definición geométrica de un vector: El conjunto de todos los segmentos de recta dirigidos equivalentemente a un segmento dirigido dado, se llama vector. Cualquier segmento de recta dirigido en ese conjunto se conoce como un represente del vector.
Tipo de vectores
a) Vector Regular: consta de un solo renglón y n columnas.
b) Vector Columna: consta de n renglones y una sola columna. 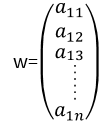
c) Vector transpuesto: proporcionar una alternativa para la multiplicación de vectores.
d) vector unitario: es aquel cuya magnitud es igual a 1.
|
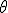 = b / a
= b / a