Los elementos de Rⁿ admiten una representación e interpretación geométrica y son la herramienta matemática básica para la manipulación de puntos, coordenadas, vectores, planos, rectas y otros muchos elementos indispensables tanto en matemáticas como en otras materias.

Puntos y vectores en Rⁿ. Intrepretación geométrica.

Los elementos de Rⁿ admiten principalmente dos representaciones geométricas. Una de ellas, como punto de una recta, plano o espacio y otra como vector o segmento orientado.

En realidad, solamente es posible representar geométricamente los conjuntos R² y R³ y, de forma más limitada, R⁴.

Puntos en Rⁿ.

La primera forma en que podemos representar una upla es en forma de punto.

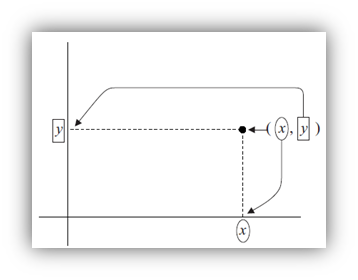
Puntos en R². El plano real.

Los elementos de R² son 2-uplas o pares como por ejemplo (2,3), (3, −1), (0,4). Su representación se efectúa sobre un plano en el cual trazamos dos ejes perpendiculares, uno horizontal, usualmente denominado eje de abcisas, y otro vertical, denominado eje de ordenadas que se cortan en un punto denominado origen u origen de coordenadas.

El primer número del par se representa en el eje horizontal y el segundo en el vertical. Así, para representar la upla genérica (x, y) marcaremos x en el eje horizontal y marcaremos y en el vertical del siguiente modo:

El eje horizontal suele denominarse también eje x y el vertical eje y.

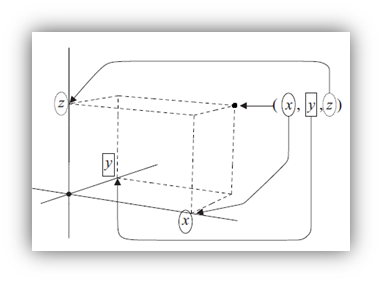
  Puntos en R³. El espacio real.

Cada elemento de R³ o 3-upla tiene 3 componentes (por ejemplo (3, 2, 1) es una 3-upla cuya primera componente es 3, la segunda es 2 y la tercera es 1).

Para representar R³ necesitamos un espacio tridimensional en el que trazamos tres ejes perpendiculares que se cruzan en un punto que llamamos nuevamente origen.
Cada una de las tres componentes de una tres upla se representará en el eje que le corresponde. Los dos ejes horizontales son para las dos primeras componentes y el eje vertical es para la tercera.

Nuevamente, el signo negativo de las componentes indicará a qué lado del origen, en cada eje, se sitúa el punto que representa a la upla en cuestión.

De hecho, los tres ejes suelen denominarse ejes x, y y z, siendo el eje x el que se utiliza para representar la primera componente, el eje y para la segunda y el eje z para la tercera.

Puntos en Rⁿ. Espacio real n-dimensional.

Para representar una 2-upla de R² necesitamos dos ejes perpendiculares dentro de un plano, por su lado, la representación de las 3-uplas de R³ se realiza sobre tres ejes perpendiculares dentro del espacio tridimensional.

Utilizando estas ideas podríamos intentar imaginar cuál sería la representación de un 4-upla de R⁴, de una 5-upla de R⁵ o en general de una n-upla de Rⁿ. El problema ahora es que para representar una 4-upla necesitaríamos cuatro ejes perpendiculares dentro de un espacio cuatridimensional y tal cosa no es materializable en la realidad ya que evidentemente nos movemos dentro de un espacio que ´únicamente’ es tridimensional.

Dicho de otro modo, no es posible realizar una representación efectiva de las uplas de R⁴, R⁵ o, en general, de Rⁿ. A pesar de ello, las ideas que hemos utilizado para R² y R³ nos permiten imaginar o intuir que esas uplas de R⁴, R⁵ o de Rⁿ se representan igualmente como puntos trazados sobre un sistema de 4, 5 o n ejes perpendiculares dentro de un espacio n-dimensional.
Es por ello que Rⁿ se denomina espacio n-dimensional real y a sus uplas las llamamos también puntos ya que podemos imaginar su representación en forma de punto.